Google is racing to develop quantum enhanced processors that utilize quantum mechanical effects to one day dramatically increase the speed at which data can be processed.
In the near term, Google has devised new quantum enhanced algorithms that operate in the presence of realistic noise. The so called quantum approximate optimisation algorithm, or QAOA for short, is the cornerstone of a modern drive towards noise-tolerant quantum enhanced algorithm development.
The celebrated approach taken by Google in QAOA has sparked vast commercial interest and ignited a global research community to explore novel applications (see ref.. Yet, little actually remains known about the ultimate performance limitations of Google’s QAOA algorithm.
A team of scientists, hailing from Skoltech’s Deep Quantum Laboratory in Center for Photonics and Quantum Materials, took up this contemporary challenge. The all-Skoltech team led by Prof. Jacob Biamonte discovered and quantified what appears to be a fundamental limitation in the wildly adopted approach initiated by Google.
Reporting in Physical Review Letters, the authors detail the discovery of so called reachability deficits – the authors show how these deficits place a fundamental limitation on the ability of QAOA to even approximate a solution to a problem instance.
Authors of the study included Skoltech doctoral students, writing as V. Akshay and Hariphan Philathong, who joined Skoltech just over a year ago. Prior to Skoltech, Akshay won the C.V Raman award for his master’s thesis in photonics from Cochin University of Science and Technology, India. Hariphan joined Skoltech after finishing his master’s degree in fundamental physics from Imperial College London as a Development and Promotion of Science and Technology (DPST) scholar from Thailand. Akshay is originally from Kerala, India, while Hariphan calls Kamphaeng Phet, Thailand, his home. Jacob Biamonte is an American from the Pacific Northwest of the United States and is considered among the world’s leading quantum algorithms experts.
The Skoltech team’s findings report a clear limitation of the variational QAOA quantum algorithm. QAOA and other variational quantum algorithms have proven extremely difficult to analyse using known mathematical techniques due to an internal quantum-to-classical feedback process. Namely, a given quantum computation can only run for a fixed amount of time. Inside this fixed time, a fixed number of quantum operations can be executed. QAOA seeks to iteratively utilize these quantum operations by forming a sequence of increasingly optimal approximations to minimize an objective function. The study places new limits on this process.
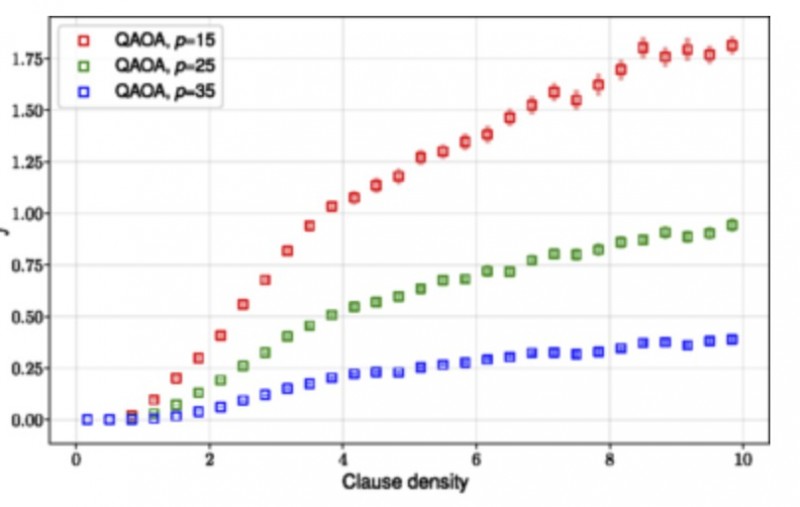
The authors discovered that QAOA’s ability to approximate optimal solutions for any fixed depth quantum circuit is fundamentally dependent on the problems “density.” In the case of the problem called MAX-SAT, the so called density can be defined as the ratio of the problems constraints to variable count. This is sometimes called clause density.
The authors discovered problem instances of high density whose optimal solutions cannot be approximated with guaranteed success, regardless of the algorithms’ run-time.
The graph represents the performance (difference between QAOA optima and exact optima) of fixed depth QAOA circuits on randomly generated MAX-SAT instances with increasing problem densities. Although higher depth versions achieve better performances, they still exhibit reachability deficits.